
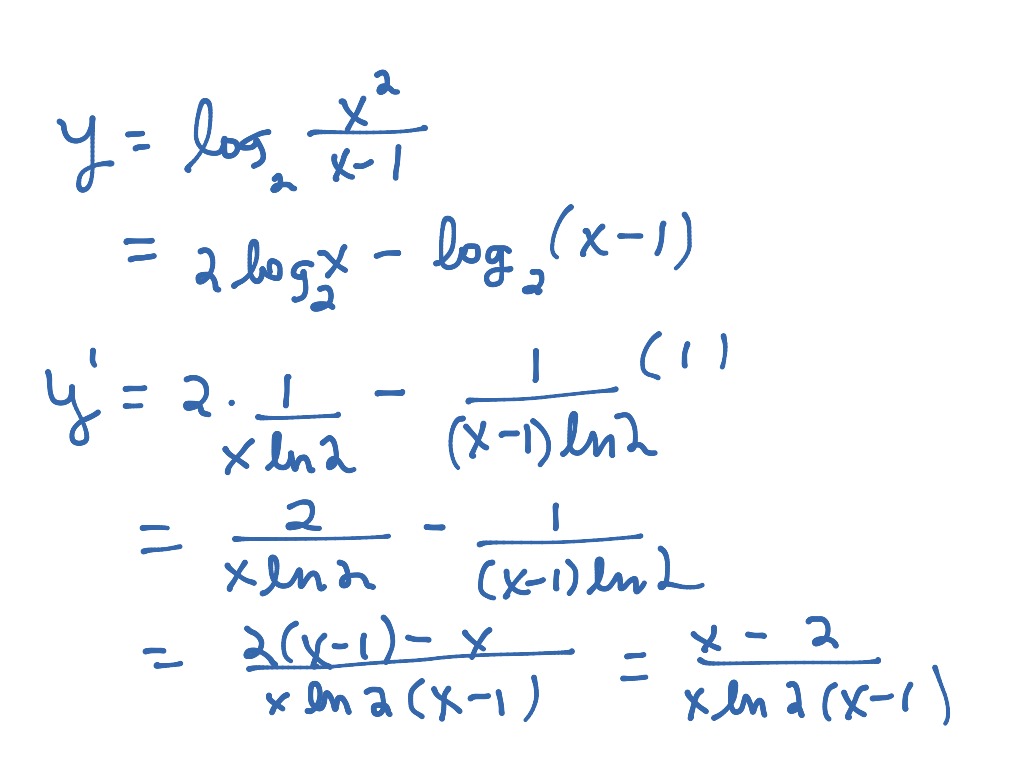
That derivative approaches 0, that is, becomes smaller.ī) when x is less than 1 and becomes smaller. A.4 Algebraic identities A.4.1 Some useful identities (i) asb + c) ab + ac. Calculate the derivative of lnĪccording to the rule for changing from base e to a different base a:Ī) when x is greater than 1 and becomes larger. When y = e u( x), then according to the chain rule:Įxample 4. The derivative of e with a functional exponent In the system of natural logarithms, in which e is the base, we have the simplest constant possible, namely 1. ( Lesson 39 of Algebra.) When we calculate that derivative below, we will see that that constant becomes ln a.
#DERIVATIVE OF LOG BASE B OF X HOW TO#
See change of base rule to see how to work out such constants on your calculator. Therefore, we conclude that the derivative of f(x)logex is f(x)1x. y log b u is a logarithm with base b, then we can obtain the derivative of the logarithm function with base b using: (dy)/(dx)(logbe)(u')/u where u' is the derivative of u. Where k is the constant of proportionality. The logarithm to the base e is an important function. Therefore, to say that the rate of growth is proportional to its size, is to say that the derivative of a x is proportional to a x. The more individuals there are, the more births there will be, and hence the greater the rate of change of the population - the number of births in each year.Īll exponential functions have the form a x, where a is the base. y log a ( x + x) log a x y log a ( x + x x) y log a ( 1 + x x) Dividing both sides by x, we get. Putting the value of function y log a x in the above equation, we get. The bigger it is at any given time, the faster it's growing at that time. The derivative of the logarithmic function is given by: f (x) 1 / ( x ln(b) ). First we take the increment or small change in the function: y + y log a ( x + x) y log a ( x + x) y. For we say that a quantity grows "exponentially" when it grows at a rate that is proportional to its size. A logarithm with base 10 is called a common logarithm, and it is expressed as log ( x ). What does that imply? It implies the meaning of exponential growth.


 0 kommentar(er)
0 kommentar(er)
